“2乘4等于几?”这听起来非常简单,但你是否想过你的大脑是如何完成这道算数题的?在本文中,你将了解到大脑用来解决算术问题的两种策略,以及你在使用这两种策略时,不同的大脑区域(如顶内沟,intraparietal sulcus)是如何协同工作的。随着你算术熟练度的增加,你使用的策略和参与算数的脑区会随着时间的推移而发生变化。这种转变在脑区的工作方式以及与其他脑区的交流方式方面尤为明显——有的脑区变得更加活跃,而其他脑区则变得不那么活跃。读完这篇文章后,你将进一步了解到大脑用来解决算术题技巧,以及完成下次数学作业所需的脑区。
引言
数学是我们需要掌握的最重要的技能之一,了解大脑如何算算术会给我们带来巨大影响。你在学校里每天都需要数学,走出校园后亦是如此。如果你想成为一个程序员、工程师或科学家,你每天都会和数字打交道。数学对几乎所有工作都很重要,所以数学逊色的人有时很难找到工作。他们中的一些人甚至可能患有所谓的发展性计算障碍(developmental dyscalculia)。因此,理解在计算时脑中发生了什么,不仅对于数学学习困难的孩子来说非常有帮助,还可以让教师以一种让孩子更容易学习的方式来组织他们的课程。当然,仅仅对事物的运作方式感到好奇就足以开展实验!
一题多解
为了研究算数,研究者要求儿童和成人算得既快又准,题目通常在计算机屏幕上逐一呈现(见图1)。参与者提供答案后,下一个问题就会出现。为了研究人们在算术过程中使用的不同策略,科学家通常会混合不同难度的算术题。

图1 - 在研究中用来调查算术问题解决能力的示例装置。
参与者在计算机屏幕上看到一个算术问题。一旦给出答案,屏幕上就会出现一个新问题。对于每个问题,研究者记录解决问题所需的时间(速度)以及答案是否正确(准确性)。
应用不同方法策略,科学家们发现算术问题可以大致分为两类:小问题和大问题。小问题(比如计算“2 × 4”)解决得很快,参与者在解决这些问题时犯的错误较少;而大问题(比如计算“12 × 3”)通常更难解决,需要更长的时间,并且也会犯更多的错误。有时,科学家们对于如何划分小问题和大问题存在分歧,原因在于解决问题的难度取决于一个人的年龄和能力。然而,解决小问题和大问题的速度和错误差别表明人们会使用两种不同的策略来解决问题。
第一种策略是计算出答案,通常用于大问题,被称为程序策略。因为得出答案涉及多个步骤或多个程序,例如,为了解决“12 × 3”,你可能会将问题分解为两个更简单的乘式,比如“10 × 3 = 30”和“2 × 3 = 6”。之后,你会将结果加起来得到答案“36”。但是增加额外的步骤也有其缺点,这既会花费更多时间,也会增加犯错误的可能。然而,你不会永远使用相同的策略来解决同一个问题。多次计算后,正确的答案某天会突然浮现在你的脑海中,这表明你解决这个问题的方式已经发生了改变。
我们来看第二种策略:凭感觉计算答案,通常被称为事实提取。通过多次练习同一个问题,你将答案存储在你的长期记忆中。从使用程序策略转变为使用事实提取是算术能力发展过程中的重要一步[3]。现在,你不用再计算答案,而是能够一下记住它。此外,通过解决简单的问题,你也会变得更擅长解决难题。为了更好地理解这些变化,我们需要观察大脑在做算术题时内部发生了什么。为此,科学家使用了多种工具,如脑电图(EEG)和功能磁共振成像(fMRI,见图2)。
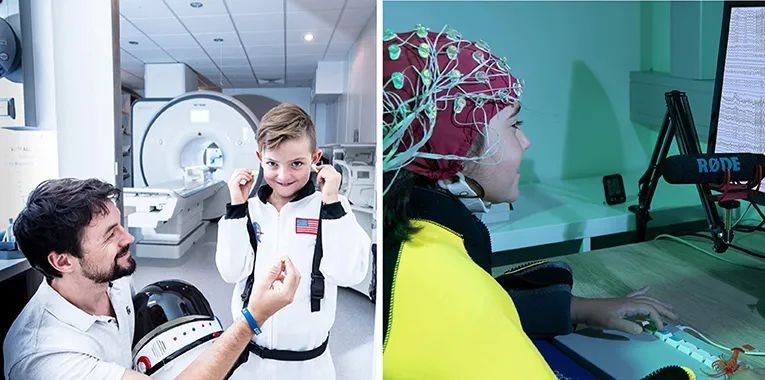
图2 - 儿童参与我们的功能磁共振成像(fMRI,左)和脑电图(EEG,右)研究。这两种工具让科学家们在大脑工作时进行研究。
大脑哪些脑区参与了算术计算?
理解大脑的工作方式有时会感觉像是完成一个复杂的拼图。就像拼图由不同的部分组成一样,我们的大脑也由不同的脑区组成(见图3)。理解每个脑区的功能,能让你更清楚地了解不同脑区是如何协同工作的。
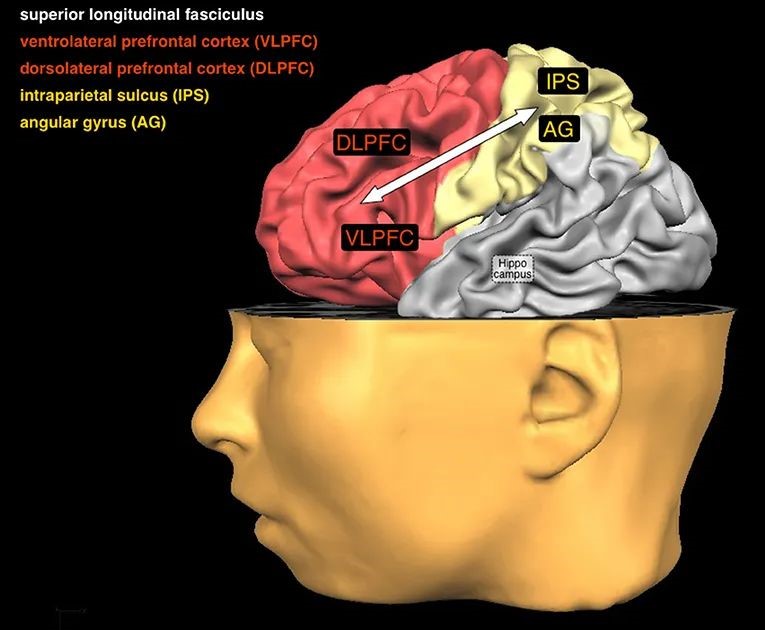
图3 - 在这张图中,您可以看到一些对算术很重要的大脑区域和一个连接。
其中两个位于前额皮层(红色),另外两个位于顶叶皮层(黄色)。它们在你进行计算时如何协同工作取决于你的年龄和能力。另一个重要的大脑区域是海马体(白色),它位于大脑的中心深处,从外部看不到。
第一块拼图是叫做顶内沟的脑区,它位于顶叶皮层(IPS,见图3),负责理解数字的含义。算术题的第一步便是理解一个数字的大小[4]。例如,你必须知道“4只狗”比“2只狗”多,而后你需要理解数字的顺序(即“1”在“2”之前,“2”在“3”之前,依此类推)。在计算时,你通过理解数字大小和顺序来找到正确的答案。
下一块拼图涉及到前额叶皮层的三大脑区:腹外侧前额叶皮层(VLPFC,见图3)与顶叶皮层一起工作,以消除干扰,例如你会畅想与朋友进行下一次骑行;背外侧前额叶皮层(DLPFC,见图3)负责操纵数字,例如将一个大问题分解成更简单的步骤;而额下回在判断看似正确实则错误的答案时发挥了关键性作用[5]。
拼图的最后两块是海马和角回。海马位于你的大脑深处,它在存储算术答案过程中起到十分重要的作用[6],海马是我们大脑的“保存”按钮。当你在做数学题时,它会与前额叶皮层一同开展工作,帮助你将答案存储在长期记忆中。然后在你进行计算时,角回会参与查找那些答案。
解决算术问题的方式是如何随龄变化的?
你是否曾和朋友一起拼过颇有挑战的拼图?倘若有,你们可能会一起合作来应对挑战。我们大脑的工作方式也是如此。在解决问题时,不同的脑区会协同工作。完成拼图的最后一步,是需要理解不同脑区在计算时是如何协同工作的。如你所知,随着年龄的增长,算算数的方式也会发生变化。你开始更频繁地使用事实提取,而不是运用程序策略来解算术题。但这并不是唯一发生变化的情形。科学家发现,在这个过程中,不同脑区之间协同工作的方式也会发生变化。例如,当你还年轻时,前额叶皮层起着非常重要的作用。它负责管理你的工作记忆和注意力,因为你解决算术问题的方式涉及多个步骤(即程序策略)。随着年龄的增长,你开始使用事实提取方法,同时,前额叶皮层也发生了变化。当你使用fMRI或EEG观察前额叶皮层时,你会发现它的活跃度在随龄减少,尽管仍然参与寻找正确答案,但它不需要像以前那般努力。也许你在与朋友合作过程中有过类似的经验。起初,你们中的某个人可能需要密切关注大家的进展,并给出下一步的指示(类似于前额叶皮层)。但是,当你们成功解决了某些问题后,就无需有人时刻检查工作情况的进展。与此同时,海马的角色也发生了变化。在事实提取过程中,儿童的海马的活跃度比成人更高。这是因为当你年纪小时,海马在努力将算术题的答案保存到你的长期记忆中。而随着年龄的增长,你的海马工作得越来越少,因为你需要保存的新答案也越来越少。
大脑中不同脑区通过相互沟通来协调工作,这种沟通是通过广泛的网络路径(称为白质)完成的,该网络连接了大脑的不同脑区。这些网络就像连接城市的道路方式一样。其中,大脑中上纵束(superior longitudinal casciculus,见图3)连接了前额叶皮层和顶叶皮层(其中包括IPS)[8]。在你生命中的某些时刻,不同的脑区参与了算术题的过程,因而这些脑区之间的连接也会发生变化。科学家们仍在试图理解这些连接为何会随龄发生变化。这意味着,尽管我们已经知道了很多关于大脑是如何算算术的,但我们仍然需要开展更多的研究来完成“算数大脑”的拼图。
结语
即使算算数听起来像是一个简单的事情,但实际上解决一个算术题涉及很多步骤。不仅如此,慢慢地你会使用不同策略来尝试解题,几乎我们大脑中的每一个细胞都会发生变化。起初,许多脑区一起工作来解决一个算术题,有的脑区让你专注于任务本身,其他脑区会跟踪并记住你的计算结果,而海马将正确的结果保存在你的长期记忆中。随着年岁的增长,你只需要几个专门的脑区来解决同样的问题,你的大脑会工作得越来越高效。在你下一次做数学作业时,请花一分钟时间感谢所有参与计算工作的脑区们!
术语表 Glossary
发展性计算困难症(Developmental Dyscalculia):是在学习或理解算术时的困难。要获得一个好的概述,请查看Young Minds的文章;当你的大脑不能做2 + 2时:一个发展性计算困难症的案例。
脑电图 (Electroencephalography,EEG):一个神经科学工具,用于测量大脑产生的电信号。这种方法可以准确地告诉我们大脑的哪个区域在什么时间点正在执行某一特定的任务。
功能磁共振成像 (Functional Magnetic Resonance Imaging, fMRI):一个用于测量大脑中耗氧差异的工具。因为活跃的脑区在任务过程中需要更多的氧气,所以我们可以准确地知道哪些脑区正在工作。
脑区(Brain Areas):大脑可以首先分为四个主要的脑叶皮层,即前额叶皮层、顶叶皮层、颞叶皮层和枕叶皮层,每一脑叶皮层又包含具有独特功能的不同脑区。
参考文献 References
[1] Bugden, S., and Ansari, D. 2014. When your brain cannot do 2 + 2: a case of developmental dyscalculia. Front. Young Minds 2:8. doi: 10.3389/frym.2014.00008
[2] Siegler, R. S. 1996. Emerging Minds: The Process of Change in Children’s Thinking. New York, NY: Oxford University Press. doi: 10.5860/choice.34-5984
[3] De Smedt, B. 2016. “Individual differences in arithmetic fact retrieval,” in Mathematical Cognition and Learning, eds D. B. Berch, D. C. Geary, and K. M. Koepke (San Diego, CA: Academic Press). p. 219–43. doi: 10.1016/B978-0-12-801871-2.00009-5
[4] Vogel, S. E., Goffin, C., and Ansari, D. 2015. Developmental specialization of the left parietal cortex for the semantic representation of Arabic numerals: an fMR-adaptation study. Dev. Cogn. Neurosci. 12, 61–73. doi: 10.1016/j.dcn.2014.12.001
[5] De Visscher, A., Vogel, S. E., Reishofer, G., Hassler, E., Koschutnig, K., De Smedt, B., et al. 2018. Interference and problem size effect in multiplication fact solving: individual differences in brain activations and arithmetic performance. Neuroimage 15:718–27. doi: 10.1016/j.neuroimage.2018.01.060
[6] Qin, S., Cho, S., Chen, T., Rosenberg-Lee, M., Geary, D. C., and Menon, V. 2014. Hippocampal-neocortical functional reorganization underlies children’s cognitive development. Nat. Neurosci. 17:1263–9. doi: 10.1038/nn.3788
[7] Cho, S., Metcalfe, A. W. S., Young, C. B., Ryali, S., Geary, D. C., and Menon, V. 2012. Hippocampal–prefrontal engagement and dynamic causal interactions in the maturation of children’s fact retrieval. J. Cogn. Neurosci. 24:1849–66. doi: 10.1162/jocn_a_00246
[8] Matejko, A. A., and Ansari, D. 2015. Drawing connections between white matter and numerical and mathematical cognition: a literature review. Neurosci. Biobehav. Rev. 1:35–52. doi: 10.1016/j.neubiorev.2014.11.006
引文 Citation
Koren N, Scheucher J and Vogel S (2020) How Much Is 2 × 4? Understanding How the Brain Solves Arithmetic Problems. Front. Young Minds. 8:48. doi: 10.3389/frym.2020.00048
中文引文 Chinese Citation
Koren N, Scheucher J and Vogel S (2020) “2乘4等于几?”——大脑如何算算术. Front. Young Minds. 8:48. doi: 10.3389/frym.2020.00048
作者 Authors
Nikolaus Koren,Judith Scheucher,Stephan E. Vogel
小小评阅人 Young Reviewers
Lijia, 12岁
Dr. H. Bavinck school, 8-12岁
编辑 Editor
Sabine Peters
科学顾问 Science Mentors
Sok King Ong
中文翻译&编辑
罗崇静 陆秋宇
中文审校
左西年 张蕾